Hiperboloide de dos hojas // Gráfico tridimensional y aplicación
En esta oportunidad voy a tratar otra aplicación más de las superficies cuádricas, tal es el caso del hiperboloide de dos hojas. No solamente explicare sus aplicaciones, sino que también realizaremos todas las especificaciones geométricas del caso, su ecuación cartesiana, el tipo de gráfico que se da en cada uno de los planos cartesianos, y finalmente el gráfico del hiperboloide de dos hojas empleando el software matemático de geogebra 5.0 .
El hiperboloide de dos hojas se origina al graficar la figura resultante de las trazas en los planos cartesianos: xy, xz, yz tomando en cuenta la siguiente ecuación:

Una consideración muy importante, es que la ecuación del hiperboloide de dos hojas es la misma que la del hiperboloide de una hoja, a excepción que tiene otra variable más negativa, esto hace de que no exista traza en dos planos, o mejor dicho que solo exista traza para un solo eje, este eje va a ser el que este positivo, para el caso de la ecuación que estamos contemplando, no va existir traza en los ejes y e z, solo va existir traza en el eje x.
Trazas en los planos cartesianos
- En el plano xy se gráfica una hipérbola, considerando que para graficar en el plano xy es bajo la consideración de que z=0, por lo que para graficar en este plano cartesiano sería bajo la siguiente ecuación:
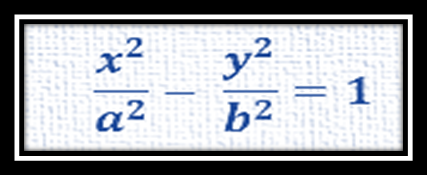
- En el plano xz se gráfica otra hipérbola considerando que para graficar en el plano xz es bajo la consideración de que y=0, por lo que para graficar en este plano cartesiano sería bajo la siguiente ecuación:
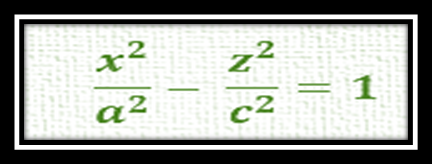
- En el plano yz no existe traza, considerando que para graficar en el plano yz es bajo la consideración de que x=0, por lo que para graficar en este plano cartesiano sería bajo la siguiente ecuación:
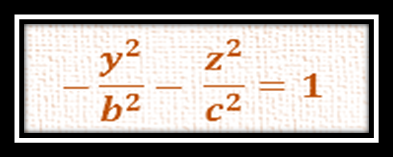
La razón por la que no existe traza, es porque las dos variables están negativas, y cuando vamos a encontrar los cortes con los ejes coordenados, hacemos una variable cero, y la que nos queda es negativa, despejamos el valor de la variable resultante, quedando al final la raíz cuadrada de un valor negativo, lo que representa es que no tiene trazas ni para el eje y ni para el eje z.
En este caso la ecuación cartesiana para el hiperboloide de dos hojas contempla que el eje del hiperboloide pertenece a la variable cuyo coeficiente es positivo, por lo que no existe traza en el plano perpendicular a este eje, para el caso de la ecuación cartesiana planteada en este caso, la variable positiva es la x, por lo tanto el eje del hiperboloide de dos hojas será el eje x, por lo que no va existir trazas en el plano yz.
Gráfico del hiperboloide de dos hojas
Para plantear la gráfica del hiperboloide, implementaremos como de costumbre el software geogebra 5.0, para ello nos planteamos un ejemplo de ecuación equivalente a la ecuación cartesiana planteada anteriormente, para ello graficamos la siguiente ecuación:
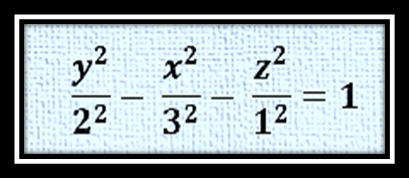
Antes de mostrar el gráfico es importante resaltar que el eje del hiperboloide en este caso es el eje y, ya que es la variable que está con signo positivo, lo otro es que en el plano cartesiano xz no va existir trazas, ya que son las variables x y z las que están con signo negativo.
Aplicaciones del hiperboloide de dos hojas
Gracias a la geometría hiperbólica, tanto el hiperboloide de una hoja como el de dos hojas, se han podido construir numerosas estructuras con forma de hiperboloide (una hoja y dos hojas).
La curva que se genera hacia el interior del hiperboloide o hacia el exterior da soporte estructural y estética a las construcciones, y además la superficie en la que se soporta esta forma geométrica es doblemente reglada lo que significa que se puede realizar con un entramado de vigas rectas.
Debido a estas consideraciones cualquier objeto que forma la forma de un hiperboloide (dos hojas o una hoja) son más fáciles de construir y más resistentes que las estructuras curvadas, las cuales necesitan vigas curvas para su construcción.
Si quisiéramos comparar la forma geométrica del hiperboloide de dos hojas, la pudiéramos asociar a la forma geométrica del reloj de arena:

Bibliografía consultada
- Cálculo con Geometría analítica de Larson y Hostetler: Volumen II.