Machine Learning

---

Mid-Level Visual Representations Improve Generalization and Sample Efficiency for Learning Visuomotor Policies (1812.11971v2)

Alexander Sax, Bradley Emi, Amir R. Zamir, Leonidas Guibas, Silvio Savarese, Jitendra Malik

2018-12-31

How much does having visual priors about the world (e.g. the fact that the world is 3D) assist in learning to perform downstream motor tasks (e.g. delivering a package)? We study this question by integrating a generic perceptual skill set (e.g. a distance estimator, an edge detector, etc.) within a reinforcement learning framework--see Figure 1. This skill set (hereafter mid-level perception) provides the policy with a more processed state of the world compared to raw images. We find that using a mid-level perception confers significant advantages over training end-to-end from scratch (i.e. not leveraging priors) in navigation-oriented tasks. Agents are able to generalize to situations where the from-scratch approach fails and training becomes significantly more sample efficient. However, we show that realizing these gains requires careful selection of the mid-level perceptual skills. Therefore, we refine our findings into an efficient max-coverage feature set that can be adopted in lieu of raw images. We perform our study in completely separate buildings for training and testing and compare against visually blind baseline policies and state-of-the-art feature learning methods.

Data-dependent PAC-Bayes priors via differential privacy (1802.09583v2)

Gintare Karolina Dziugaite, Daniel M. Roy

2018-02-26

The Probably Approximately Correct (PAC) Bayes framework (McAllester, 1999) can incorporate knowledge about the learning algorithm and (data) distribution through the use of distribution-dependent priors, yielding tighter generalization bounds on data-dependent posteriors. Using this flexibility, however, is difficult, especially when the data distribution is presumed to be unknown. We show how an {\epsilon}-differentially private data-dependent prior yields a valid PAC-Bayes bound, and then show how non-private mechanisms for choosing priors can also yield generalization bounds. As an application of this result, we show that a Gaussian prior mean chosen via stochastic gradient Langevin dynamics (SGLD; Welling and Teh, 2011) leads to a valid PAC-Bayes bound given control of the 2-Wasserstein distance to an {\epsilon}-differentially private stationary distribution. We study our data-dependent bounds empirically, and show that they can be nonvacuous even when other distribution-dependent bounds are vacuous.

SSRGD: Simple Stochastic Recursive Gradient Descent for Escaping Saddle Points (1904.09265v1)

Zhize Li

2019-04-19

We analyze stochastic gradient algorithms for optimizing nonconvex problems. In particular, our goal is to find local minima (second-order stationary points) instead of just finding first-order stationary points which may be some bad unstable saddle points. We show that a simple perturbed version of stochastic recursive gradient descent algorithm (called SSRGD) can find an -second-order stationary point with stochastic gradient complexity for nonconvex finite-sum problems. As a by-product, SSRGD finds an -first-order stationary point with stochastic gradients. These results are almost optimal since Fang et al. [2018] provided a lower bound for finding even just an -first-order stationary point. We emphasize that SSRGD algorithm for finding second-order stationary points is as simple as for finding first-order stationary points just by adding a uniform perturbation sometimes, while all other algorithms for finding second-order stationary points with similar gradient complexity need to combine with a negative-curvature search subroutine (e.g., Neon2 [Allen-Zhu and Li, 2018]). Moreover, the simple SSRGD algorithm gets a simpler analysis. Besides, we also extend our results from nonconvex finite-sum problems to nonconvex online (expectation) problems, and prove the corresponding convergence results.

On the Convergence of Adam and Beyond (1904.09237v1)

Sashank J. Reddi, Satyen Kale, Sanjiv Kumar

2019-04-19

Several recently proposed stochastic optimization methods that have been successfully used in training deep networks such as RMSProp, Adam, Adadelta, Nadam are based on using gradient updates scaled by square roots of exponential moving averages of squared past gradients. In many applications, e.g. learning with large output spaces, it has been empirically observed that these algorithms fail to converge to an optimal solution (or a critical point in nonconvex settings). We show that one cause for such failures is the exponential moving average used in the algorithms. We provide an explicit example of a simple convex optimization setting where Adam does not converge to the optimal solution, and describe the precise problems with the previous analysis of Adam algorithm. Our analysis suggests that the convergence issues can be fixed by endowing such algorithms with `long-term memory' of past gradients, and propose new variants of the Adam algorithm which not only fix the convergence issues but often also lead to improved empirical performance.

Modeling Human Decision-making in Generalized Gaussian Multi-armed Bandits (1307.6134v4)

Paul Reverdy, Vaibhav Srivastava, Naomi E. Leonard

2013-07-23

We present a formal model of human decision-making in explore-exploit tasks using the context of multi-armed bandit problems, where the decision-maker must choose among multiple options with uncertain rewards. We address the standard multi-armed bandit problem, the multi-armed bandit problem with transition costs, and the multi-armed bandit problem on graphs. We focus on the case of Gaussian rewards in a setting where the decision-maker uses Bayesian inference to estimate the reward values. We model the decision-maker's prior knowledge with the Bayesian prior on the mean reward. We develop the upper credible limit (UCL) algorithm for the standard multi-armed bandit problem and show that this deterministic algorithm achieves logarithmic cumulative expected regret, which is optimal performance for uninformative priors. We show how good priors and good assumptions on the correlation structure among arms can greatly enhance decision-making performance, even over short time horizons. We extend to the stochastic UCL algorithm and draw several connections to human decision-making behavior. We present empirical data from human experiments and show that human performance is efficiently captured by the stochastic UCL algorithm with appropriate parameters. For the multi-armed bandit problem with transition costs and the multi-armed bandit problem on graphs, we generalize the UCL algorithm to the block UCL algorithm and the graphical block UCL algorithm, respectively. We show that these algorithms also achieve logarithmic cumulative expected regret and require a sub-logarithmic expected number of transitions among arms. We further illustrate the performance of these algorithms with numerical examples. NB: Appendix G included in this version details minor modifications that correct for an oversight in the previously-published proofs. The remainder of the text reflects the published work.

Machine learning for early prediction of circulatory failure in the intensive care unit (1904.07990v2)

Stephanie L. Hyland, Martin Faltys, Matthias Hüser, Xinrui Lyu, Thomas Gumbsch, Cristóbal Esteban, Christian Bock, Max Horn, Michael Moor, Bastian Rieck, Marc Zimmermann, Dean Bodenham, Karsten Borgwardt, Gunnar Rätsch, Tobias M. Merz

2019-04-16

Intensive care clinicians are presented with large quantities of patient information and measurements from a multitude of monitoring systems. The limited ability of humans to process such complex information hinders physicians to readily recognize and act on early signs of patient deterioration. We used machine learning to develop an early warning system for circulatory failure based on a high-resolution ICU database with 240 patient years of data. This automatic system predicts 90.0% of circulatory failure events (prevalence 3.1%), with 81.8% identified more than two hours in advance, resulting in an area under the receiver operating characteristic curve of 94.0% and area under the precision-recall curve of 63.0%. The model was externally validated in a large independent patient cohort.

Partial recovery bounds for clustering with the relaxed 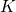means (1807.07547v3)

Christophe Giraud, Nicolas Verzelen

2018-07-19

We investigate the clustering performances of the relaxed means in the setting of sub-Gaussian Mixture Model (sGMM) and Stochastic Block Model (SBM). After identifying the appropriate signal-to-noise ratio (SNR), we prove that the misclassification error decay exponentially fast with respect to this SNR. These partial recovery bounds for the relaxed means improve upon results currently known in the sGMM setting. In the SBM setting, applying the relaxed means SDP allows to handle general connection probabilities whereas other SDPs investigated in the literature are restricted to the assortative case (where within group probabilities are larger than between group probabilities). Again, this partial recovery bound complements the state-of-the-art results. All together, these results put forward the versatility of the relaxed means.

Reliable Multi-label Classification: Prediction with Partial Abstention (1904.09235v1)

Vu-Linh Nguyen, Eyke Hüllermeier

2019-04-19

In contrast to conventional (single-label) classification, the setting of multi-label classification (MLC) allows an instance to belong to several classes simultaneously. Thus, instead of selecting a single class label, predictions take the form of a subset of all labels. In this paper, we study an extension of the setting of MLC, in which the learner is allowed to partially abstain from a prediction, that is, to deliver predictions on some but not necessarily all class labels. We propose a formalization of MLC with abstention in terms of a generalized loss minimization problem and present first results for the case of the Hamming and rank loss, both theoretical and experimental.

Uncertainty about Uncertainty: Near-Optimal Adaptive Algorithms for Estimating Binary Mixtures of Unknown Coins (1904.09228v1)

Jasper C. H. Lee, Paul Valiant

2019-04-19

Given a mixture between two populations of coins, "positive" coins that have (unknown and potentially different) probabilities of heads and negative coins with probabilities , we consider the task of estimating the fraction of coins of each type to within additive error . We introduce new techniques to show a fully-adaptive lower bound of samples (for constant probability of success). We achieve almost-matching algorithmic performance of samples, which matches the lower bound except in the regime where . The fine-grained adaptive flavor of both our algorithm and lower bound contrasts with much previous work in distributional testing and learning.

Risk Convergence of Centered Kernel Ridge Regression with Large Dimensional Data (1904.09212v1)

Khalil Elkhalil, Abla Kammoun, Xiangliang Zhang, Mohamed-Slim Alouini, Tareq Al-Naffouri

2019-04-19

This paper carries out a large dimensional analysis of a variation of kernel ridge regression that we call \emph{centered kernel ridge regression} (CKRR), also known in the literature as kernel ridge regression with offset. This modified technique is obtained by accounting for the bias in the regression problem resulting in the old kernel ridge regression but with \emph{centered} kernels. The analysis is carried out under the assumption that the data is drawn from a Gaussian distribution and heavily relies on tools from random matrix theory (RMT). Under the regime in which the data dimension and the training size grow infinitely large with fixed ratio and under some mild assumptions controlling the data statistics, we show that both the empirical and the prediction risks converge to a deterministic quantities that describe in closed form fashion the performance of CKRR in terms of the data statistics and dimensions. Inspired by this theoretical result, we subsequently build a consistent estimator of the prediction risk based on the training data which allows to optimally tune the design parameters. A key insight of the proposed analysis is the fact that asymptotically a large class of kernels achieve the same minimum prediction risk. This insight is validated with both synthetic and real data.

---