复杂气固催化过程之烷氧基硅烷的直接合成（续 1）

3. 甲醇的解离与碰撞统计

甲醇有两种键断裂方式。用 R 代记甲基 (CH₃)。在一般条件下，25 ℃时，R-OH 断裂能为 387kj/mol， RO-H 断裂能为436kj/mol，前者较容易断裂。在特定条件下，可以使 RO-H 断裂方式相对于 R-OH 断裂方式发生的机率更大。 这样考虑，其离解后的基团可能有四种：R/OR/OH/H。产物具有结构形式 H_aSiR_bOR_cOH_d, (a+b+c+d=4, 0≤a,b,c,d ≤4)------(3.1) 進一步假定(R-OH)断键方式的概率为 P₁，(RO-H)断键方式的概率为 P₂， (P₁+P₂=1) 。 则 n 个醇分子离解后产生出 nP₁个 R^- 和 nP₁ 个 OH⁺， nP₂ 个 OR^- 和 nP₂ 个 H⁺。 把 nP₁简记为 n₁，nP₂ 简记为 n₂，则 H_aSiR_bOR_cOH_d 出现的概率为： P= C^a_n1C^b_n2C^c_n1C^d_n2 / C⁴_2n------(3.2) 全部可能的产物共有 35 种。在醇硅直接合成过程中的产物的色谱分析图上可以查到 30 余个特征峰就是证据。 产物出现概率的较好的估计需要这些离子的离子半径，准确数据尚未找到。 解离方式有四种可能：

1. 极性解离；
2. 催化解离；
3. 吸附解离。
4. 不发生解离。

笔者现有的认识，本反应中的甲醇需要解离，三种解离方式都可能存在，而溶剂的极性解离作用最大。 因此，极性溶剂是必要的。溶剂除了起悬浮作用之外，最重要的作用是实现和加速甲醇的解离。 如果甲醇不能快速解离，反应不能快速按指定方向进行。 假设某种催化系统能抑制 R-OH 断裂并提高 RO-H 键的断裂概率，这种假设没有坏处。 离开催化剂，本反应几乎不发生。

4. 醇-硅过程的均相反应模型

要设计反应系统，必须设想其反应原理模型，哪怕是简化的，宏观的。 为推导与编程方便，将硅简记作 B₁(不致误会时它就是 B)， H₂B(OR)₂ 为 B₂, HB(OR)₃ 为 B₃, B(OR)₄ 为 B₄, RB(OR)₃ 为 B₅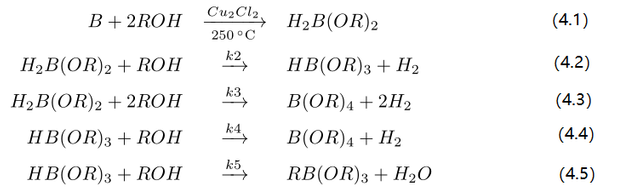

建立微分方程并求解，可以得到一组方程，（微分方程的建立与求解过程及解组放在后面的附录中。） 编写计算代码，假设一组状态参数(反应速率 k_i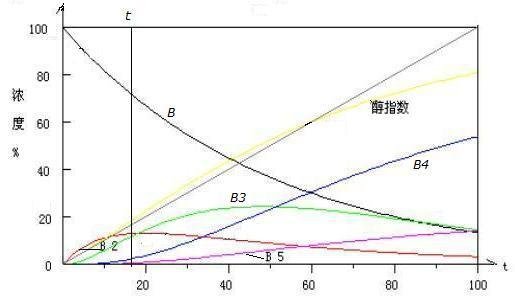

图 4.1 醇-硅过程模拟运行图

全混流反应模型本质上就是这个模式。一个是固体，一个是气体，醇-硅过程当然不是均相的。但是，我们可以借用这个模型了解过程的某些特性。 在某一试验阶段使用这一模型了解过程的基本特性是必要的。后面我们再讨论如何修正这一实验模型。 图 4.1 中的醇指数是 t 时刻 各组分(B_i)所含甲基之和摩尔数计算值， 2B₂+3B₃+4B₄+4B₅。 它与醇的实际供给量(图中左下角至右上角的斜线)不重合，醇的缺失是假的，因为这些速率的模拟是随意假设的而不是测定的。 另一方面，这一现象反映过程的本质。有一个时刻，在这个时刻之前，醇处于饥饿状态， 反应处于激烈的竞争中。之后，竞争相对不激烈，以致逐渐消失。

由图 4.1 很清楚地看出，反应(4.1)-(4.5)是复杂反应，可以分为三组：

第一组：反应主要为(4.1)的引发生成 B₂；

第二组：平行反应(4.1)、(4.3)竞争地发生，消耗醇和 B₂ 分别生成 B₃ 和 B₄；

第三组： B₃ 出现之后，平行反应(4.4)、(4.5})发生，又竞争消耗醇和 B₃ ，分别生成 B₄ 和 B₅.

组间具有串反应性质。一旦 B₂,B₃ 出现之后，这三组之间又互相竞争。竞争消耗醇和目标产物。组间已失去时序关系，发生恶性竞争。 存在一个时刻 t， B₂ 达到最大值， B₃ 随后达到最大值。B₃ 一旦出现， B₄,B₅ 即获得出现的可能， 逐渐出现并迅速增加且不减。一旦 B₅出现，就意味着有水出现了，系统将面临各种麻烦。

反应的控制在于醇。只要有醇，即使没有硅了，反应照样能够继续，直到全部组分变成 B₄或 B₅。 如果没有醇，即使有再多的硅，反应会立即停止，各种产物的浓度不会继续发生变化。 假定在某一时刻，停止加入醇。在系统逐渐消耗完剩余的甲醇之后，反应会停止。

过程开发的要求是使主产物浓度最高而副产物浓度较低。 其措施只能是选择一个恰当的时刻，停止加入醇使反应停止。将目标产物提取出来后再进入下一反应周期。

附录： 微分方程及其解

为书写方便和便于迭代计算，将硅简记作 B₁ (不至误会时，有时也记作 B)， H₂B(OR)₂ 为 B₂, HB(OR)₃ 为 B₃, B(OR)₄ 为 B₄, RB(OR)₃ 为 B₅ 。 在这一组记号下，假设反应器是一个容积足够大足以容纳全部原料和产物的全混釜。 将 M 摩尔硅粉及催化剂加入其中，并且假定每一个硅原子都以平等的身份参与反应。 以等速 v 摩尔/1分钟加入甲醇（ROH），且 v 适当大，使系统能维持 ROH 的浓度 C_Me 为常值，直到反应完成。 5 个反应，相应有 5 个反应速率 k₁,...,k₅ ，需要实验测定。在时刻 t，各组分 B_i 的浓度变化， 从(4.1)-(4.5)可以得到微分方程组

dB₁(t)/dt = -k₁B₁CMe² ------(A.1)

dB₂(t)/dt = -k₁B₁CMe² -B₂CMe ------(A.2)

dB₃(t)/dt = -k₂B₂CMe-B₃CMe(k₄+k₅) ------(A.3)

dB₄(t)/dt = -k₃B₂CMe² +k₄B₃CMe ------(A.4)

dB₅(t)/dt = k₅B₃CMe ------ (A.5)

B_i 应当满足关系

B₁+B₂+B₃+B₄+B₅=M ------(A.6)

t=0 时 B_i=0,(i=1,2,3,4,5) 。上述 5 个微分方程只有 4 个是独立的，满足关系 ∑dB_i/dt=0

在稳态操作条件下，假定甲醇的加料速度 v 适合使甲醇的浓度 CMe 是一常数，可并入 k_i 中。 可以将(A.1)- (A.5)重写作

dB₁(t)/dt = -k₁B₁ ------ (A.7)

dB₂(t)/dt = -k₁B₁-B₂ ------ (A.8)

dB₃(t)/dt = -k₂B₂-B₃(k₄+k₅) ------ (A.9)

dB₄(t)/dt = -k₃B₂+k₄B₃ ------ (A.10)

dB₅(t)/dt = k₅B₃ ------ (A.11)

这是一组线性非齐次常微分方程，逐个方程分离变量，应用常数变易法，积分结果如下。

B₁(t) = c₁exp(-k₁t)

c₁ = B₁(0)=M

B₂(t) = -c₂exp(-k₁t) + c₂ exp(-k₂₃t)

k₂₃ = k₂+k₃

c₂ = k₁c₁ / k₂₃-k₁

B₃(t) = c₃₁ exp(-k₁t)+c₃₂ exp(-k₂₃t) +c₃ exp(-k₄₅t)

k₄₅ = k₄ + k₅

c₃ = -c₃₁ -c₃₂

c₃₁ = k₂k₄₅-k₁

c₃₂=k₂c₂k₄₅-k₂₃

c₄₁ = k₄c₃₁₃c₂/-k₁

c₄₂=k₃c₂+k₄c₃₂/-k₂₃

c₄₃=k₄c₃+k₄c₃₂/-k₄₅

c₄ = - c₄₁- c₄₂- c₄₃

B₄(t) = c₄₁ exp(-k₁t)+c₄₂ exp(-k₂₃t) + c₄₃ exp(-k₄₅t)+c₄

c₅₁ = k₅c₃₁ / -k₁

c₅₂= k₅c₃₂ / -k₂₃

c₅₃= k₅c₃ / -k₄₅

c₅ = - c₅₁ - c₅₂ - c₅₃

B₅(t) = c₅₁ exp(-k₁t) + c₅₂ exp(-k₂₃t) + c₅₃ exp(-k₄₅t) + c₅

B₅(t) 也可以由(A.6)式算出。

(参考文献同 复杂气固催化过程之烷氧基硅烷的直接合成（1）)