27-08-2025 - Exercise - The Polyhedron [EN]-[IT]

Cover background image generated with AI, software used: copilot microsoft

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

[ENGLISH]
27-08-2025 - Exercise - The Polyhedron [EN]-[IT]

With this post, I would like to provide some brief information on the above topic by completing some exercises.
The context in which we operate is Operations Research
(lesson/article code: QE_08)

Linear Programming LP
Linear programming is a mathematical technique. This discipline originated in the United States around 1940/1950 and was later taught in universities. Linear programming maximizes or minimizes a linear objective function. This mathematical technique is used to solve problems involving constraints, which are equations or inequalities that represent limits on available resources.

Polyhedra
Polyhedra are extremely important in linear programming. They are geometric figures in an n-dimensional space defined as the intersection of a set of half-spaces.
Essentially, every linear constraint, such as ax + by ≤ c, defines a half-space.
When we analyze a linear programming problem, we will find that the intersection of all half-spaces will form a polyhedron.
The recession cone of a polyhedron is defined as the set of all directions of the polyhedron.

The Importance of the Polyhedron
Being able to derive or draw the polyhedron of a linear programming problem is important because the vertices of the polyhedron could be the optimal solution; that is, one of these vertices will be the best solution for our linear programming problem. The importance of the polyhedron also lies in the fact that studying it helps us understand the structure of the problem, its feasibility, and whether the solution is bounded or unbounded.

Example Linear Programming Problem
Let's say we have a problem with two variables x1 and x2 with their corresponding constraints.

x1 + x2 ≤ 5
x1 ≥ 0
x2 ≥ 0

This linear programming problem will form a polyhedron that will actually be a triangle.

This triangle has vertices (0, 0), (5, 0), and (0, 5).
The triangle will be bounded by the line x1 + x2 = 5 and the Cartesian axes.

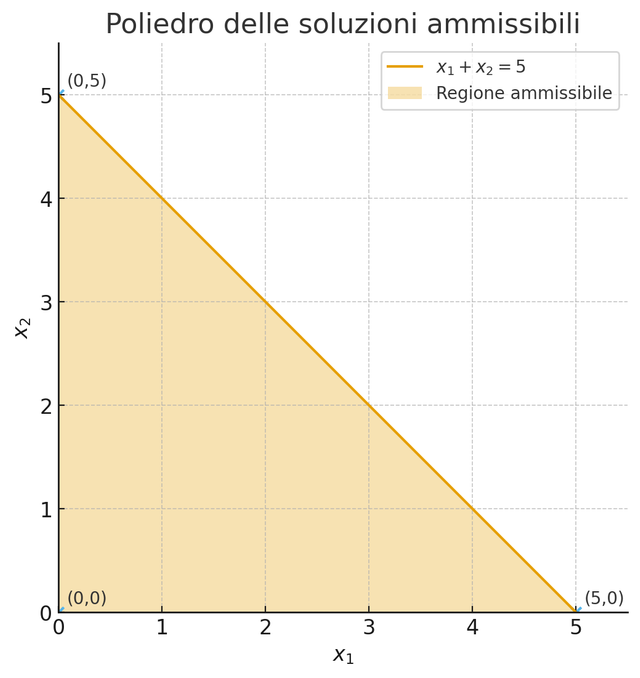
Below is the polyhedron with feasible solutions.

In this graph, the polyhedron is closed and bounded. Recall that any linear objective function admits an optimum on the boundary, specifically at a vertex.
We can say that to maximize c1x1 + c2x2
if c1>c2 we will have the optimum at the point (5, 0)
if c1<c2 we will have the optimum at the point (0, 5)
if c1=c2 we will have infinite optimums on x1+x2=5

Conclusions
In conclusion, we can say that in linear programming, the polyhedron of a linear programming problem represents all the feasible solutions. Knowing how to read the polyhedron is important because it also contains the best solution to our linear programming problem.
In other words, in linear programming, the polyhedron is simply the feasible region, that is,
the set of all vectors 𝑥 that satisfy the constraints.

Question
Have you ever heard of linear programming? Have you ever done an exercise?

---

---

[ITALIAN]
27-08-2025 - Esercizio - Il poliedro [EN]-[IT]

Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento citato in oggetto svolgendo degli esercizi.
Il contesto in cui operiamo è quello della Ricerca Operativa
(codice lezione/articolo: QE_08)

Programmazione lineare PL
La programmazione lineare è una tecnica matematica. Questa disciplina nasce negli Stati Uniti intorno al 1940/1950 per essere poi successivamente insegnata nelle università. La programmazione lineare massimizza o minimizza una funzione obiettivo lineare. Questa tecnica matematica viene usata per risolvere problemi in cui sono presenti dei vincoli, che sono equazioni o disequazioni le quali rappresentano limiti sulle risorse disponibili.

I poliedri
I poliedri nella programmazione lineari acquistano un importanza estrema. Essi sono delle figure geometriche in uno spazio n-dimensionale definita come l'intersezione di un insieme di semispazi.
Sostanzialmente ogni vincolo lineare, come potrebbe essere ax+by≤c, definisce un semispazio.
Quando andiamo ad analizzare un problema di programmazione lineare avremo che l'intersezione di tutti i semispazi formeranno un poliedro.
Si definisce cono di recessione di un poliedro l'insieme di tutte le direzioni del poliedro.

L'importanza del poliedro
Riuscire a ricavare o a disegnare il poliedro di un problema di programmazione lineare è importante perché i vertici del poliedro potrebbero essere la soluzione ottimale, cioè, uno di questi vertici sarà la soluzione migliore per il nostro problema di programmazione lineare. L'importanza del poliedro sta nel fatto anche che il suo studio aiuta a capire la struttura del problema, la fattibilità, e se la soluzione è limitata o illimitata.

Esempio di problema di programmazione lineare
Pensiamo di avere un problema con due variabili x1 e x2 con i relativi vincoli

x1 + x2 ≤ 5
x1 ≥ 0
x2 ≥ 0

Questo problema di programmazione lineare formerà un poliedro che sarà in realtà un triangolo.
Questo triangolo ha vertici (0,0), (5,0) e (0,5)
Il triangolo sarà delimitato dalla retta x1+x2=5 e dagli assi cartesiani.
Qui di seguito il poliedro delle soluzioni ammissibili

Nel caso di questo grafico, il poliedro è chiuso e limitato. Ricordiamo che qualunque funzione obiettivo lineare ammette un ottimo sul bordo, in particolare in un vertice.
Possiamo dire che per massimizzare c1x1 + c2x2
se c1>c2 avremo l'ottimo nel punto (5,0)
se c1<c2 avremo l'ottimo nel punto (0,5)
se c1=c2 avremo infiniti ottimi su x1+x2=5

Conclusioni
Possiamo dire in conclusione, che nella programmazione lineare il poliedro di un problema di programmazione lineare rappresenta tutte le soluzioni ammissibili. Saper leggere il poliedro è importante perché in esso c'è anche segnata la soluzione migliore al nostro problema di programmazione lineare.
In altre parole, in programmazione lineare, il poliedro è semplicemente la regione ammissibile, cioè
l’insieme di tutti i vettori 𝑥 che soddisfano i vincoli.

Domanda
Avete mai sentito parlare di programmazione lineare? Avete mai eseguito un esercizio?

THE END