30-09-2025 - Exercise - Simplex, the first step [EN]-[IT]
Cover background image generated with AI, software used: copilot microsoft
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
[ENGLISH]
30-09-2025 - Exercise - Simplex, the first step [EN]-[IT]
With this post, I would like to provide some brief insights into the topic mentioned above by solving some exercises.
The context in which we operate is Operations Research
(lesson/article code: MS_13)
Simplex, the first step
Regarding the field of linear programming, we can say that the most popular and most used algorithm is the simplex method.
The simplex method allows one to easily find the optimal solution to problems of medium complexity.
Without the application of this method, linear programming would be difficult to solve in some cases.
Key Point
The key point of the simplex method is the first transformation of the tableau, and below I will try to explain how it occurs.
Example
Let's take the following two-variable linear programming problem as an example.
Maximization Problem
With the following constraints
Introducing Slack Variables
Now the first thing to do is transform the problem into standard form by introducing the slack variables s1 and s2.
Our two constraints will look like this: below
The objective function, since it is a maximization problem, will be transformed as follows:
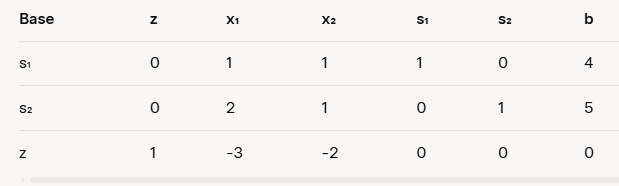
Initial Tableau
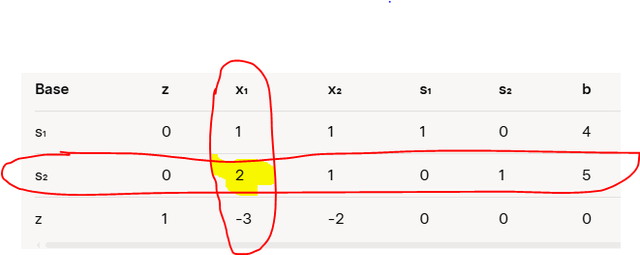
Now we can write the initial tableau with the Slack variables. Here's how it looks:
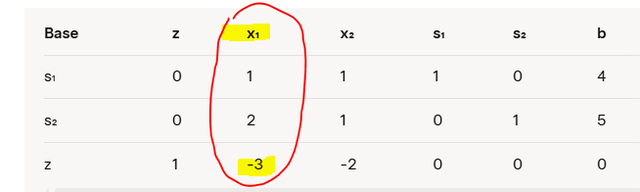
Choice of the entering variable
The entering variable will be the one in the column in which row Z has the smallest coefficient.
In our case, it will be x1.
Outgoing variable
For the outgoing variable, we need to calculate the ratios, which is:
RHS ratio (column b) / coefficient of x1)
In row 1, we have = 4/1=1
In Line 2 = 5/2=2.5 (s2 comes up)
s2 comes up because it is the smaller ratio.
Pivot
Now we need to calculate the pivot. The pivot point is found by crossing the column of the incoming variable and the row of the outgoing variable.
The pivot point is 2
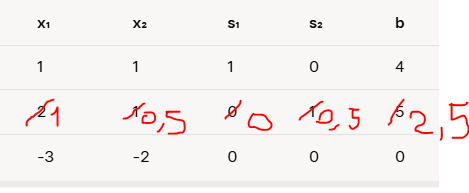
Now let's transform row 2 so that the pivot point becomes 1.
Divide row 2 by 2 and we will have the following result.
Normalization of x1
We need to cancel the coefficient of x1.
To do this, note that the Its coefficient is 1, and then we apply the following transformation.
x1 = 1 -1 * (1) = 0
x2 = 1 -1 * (0.5) = 0.5
s1 = 1 -1 * (0) = 1
s2 = 0 -1 * (0.5) = -0.5
s2 = 4 -1 * (2.5) = 1.5
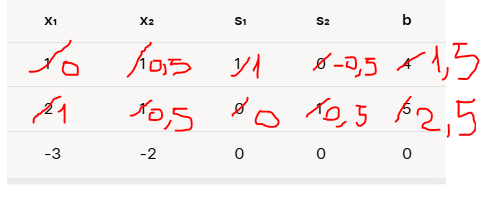
Below is the new line 1
Z Normalization
We need to cancel the coefficient of x1 in row Z, so we need to cancel the coefficient -3.
To do this, note that its coefficient is -3 and then apply the following transformation.
We always repeat the previous rule, changing the rows.
x1 = -3 -(-3) * (1) = 0
x2 = -2 -(-3) * (0.5) = 0.5
s1 = 0 -(-3) * (0) = 0
s2 = 0 -(-3) * (0.5) = 1.5
s2 = 0 -(-3) * (2.5) = 7.5
The tableau after the first pass
And here is the tableau after the first pass
Conclusions
The simplex method is one of the best-known techniques for solving linear programming problems. This method is efficient for problems with few variables and constraints, and is the basis of many optimization software.
Question
Did you know that this method is used to solve problems in economics, engineering, and business management?

[ITALIAN]
30-09-2025 - Esercizio - Simplesso, il primo passaggio [EN]-[IT]
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento citato in oggetto svolgendo degli esercizi.
Il contesto in cui operiamo è quello della Ricerca Operativa
(codice lezione/articolo: MS_13)
Simplesso, il primo passaggio
Per quanto riguarda l'ambito della programmazione lineare, possiamo dire che l'algoritmo più popolare e più usato è quello del simplesso.
Il metodo del simplesso permette di trovare facilmente la soluzione ottima in problemi con una complessità media.
Senza l'applicazione di questo metodo, in alcuni casi, la programmazione lineare risulterebbe di difficile risoluzione.
Punto chiave
Il punto chiave del metodo del simplesso è la prima trasformazione del tableau e qui di seguito proverò a spiegare come avviene.
Esempio
Prendiamo come esempio il seguente problema di programmazione lineare a due variabili.
Problema di massimizzazione
Con i seguenti vincoli
Introduzione delle variabili di slack
Ora la prima cosa da fare è trasformare il problema in forma standard introducendo le variabili di slack s1 e s2
Avremo che i nostri due vincoli appariranno come segue sotto
la funzione obiettivo, visto che è un problema di massimizzazione si trasformerà come segue:
Tableau iniziale
Ora possiamo scrivere il tableau iniziale con le variabili di slack. Qui sotto come si presenta
Scelta della variabile entrante
La variabile entrante sarà quella della colonna in cui la riga Z ha il coefficiente minore
Nel nostro caso sarà x1
Variabile uscente
Per variabile uscente dobbiamo fare il calcolo dei rapporti che è:
rapporto RHS (colonna b) / coefficiente di x1)
Nella riga 1 abbiamo = 4/1=1
Nella riga 2 abbiamo = 5/2=2,5 (esce s2)
Esce s2 in quanto è il rapporto minore
Pivot
Ora dobbiamo calcolare il pivot. Il punto Pivot è quello che troviamo tramite l'incrocio della colonna della variabile entrante e la riga della variabile uscente
Il pivot vale 2
Ora trasformiamo la riga 2 in modo che il pivot diventi 1
Dividiamo la riga 2 per 2 ed avremo il seguente risultato
Normalizzazione di x1
Dobbiamo annullare il coefficiente di x1
per fare questo notiamo che il suo coefficiente è 1 e poi applichiamo la seguente trasformazione
x1 = 1 -1 * (1) = 0
x2 = 1 -1 * (0.5) = 0,5
s1 = 1 -1 * (0) = 1
s2 = 0 -1 * (0,5) = -0,5
s2 = 4 -1 * (2,5) = 1,5
Qui di seguito la nuova riga 1
Normalizzazione di Z
Dobbiamo annullare il coefficiente di x1 nella riga Z, quindi dobbiamo annullare il coefficiente -3
per fare questo notiamo che il suo coefficiente è -3 e poi applichiamo la seguente trasformazione
Ripetiamo sempre la regola di prima cambiando le righe
x1 = -3 -(-3) * (1) = 0
x2 = -2 -(-3) * (0.5) = 0,5
s1 = 0 -(-3) * (0) = 0
s2 = 0 -(-3) * (0,5) = 1,5
s2 = 0 -(-3) * (2,5) = 7,5
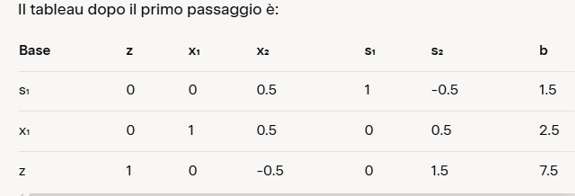
Il tableau dopo il primo passaggio
Ed ecco qua il tableu dopo il primo passaggio
Conclusioni
Il metodo del simplesso è una delle tecniche più conosciute per risolvere problemi di programmazione lineare. Questo metodo è efficiente per problemi con poche variabili e vincoli, ed è alla base di molti software di ottimizzazione.
Domanda
Sapevate che questo metodo è usato per risolvere problemi di economia, ingegneria e gestione aziendale?
THE END



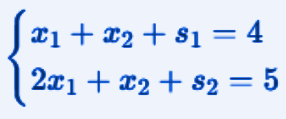
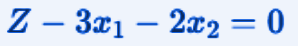
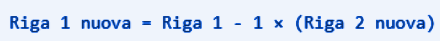

Upvoted! Thank you for supporting witness @jswit.