11-08-2025 - Education - Degrees of Freedom of a Mechanical System [EN]-[IT]
Cover background image generated with AI, software used: copilot microsoft
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
[ENGLISH]
11-08-2025 - Education - Degrees of Freedom of a Mechanical System [EN]-[IT]
With this post, I would like to provide some brief information on the topic mentioned above.
The context in which we operate is that of Applied Mechanics
(code notes: MOD-92)
Mechanical System
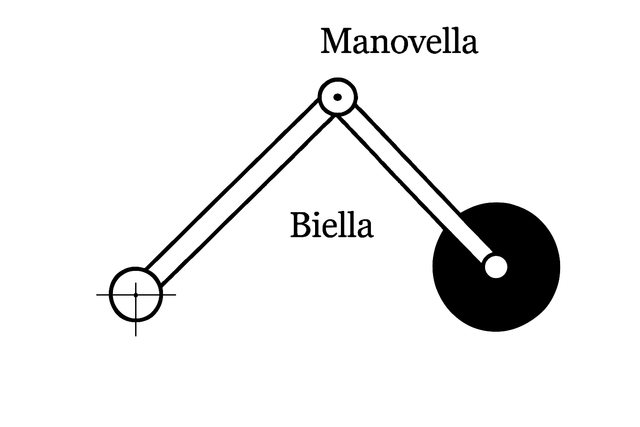
A mechanical system is a set of objects that are connected to each other and perform a movement based on constraints. The most classic example is the connecting rod and crank system.
Below is an image of the connecting rod and crank system.
Image created with artificial intelligence, the software used is Microsoft Copilot
Constraints
A mechanical system is therefore usually subject to constraints, that is, something that constrains its movement or forces a lever to move in predetermined directions.
Degrees of Freedom
In a mechanical system, degrees of freedom indicate how many independent variables are needed to completely describe the position of a mechanical system, taking into account whether the motion can be translational or rotational.
A good understanding of the degrees of freedom of a mechanical system allows you to correctly model the system's behavior. This is an essential phase in mechanical design.
Exercise
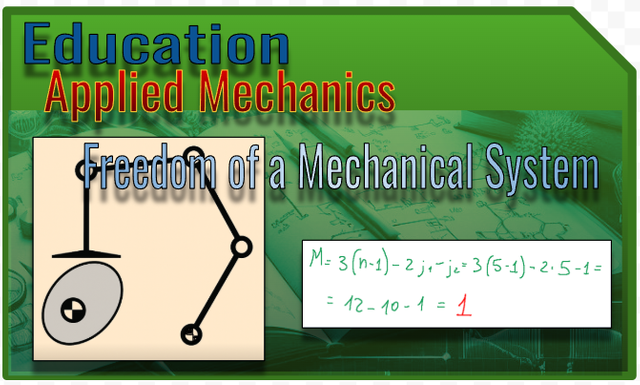
Let's take the mechanical system shown in the figure below as an example.
Let's try to understand how many degrees of freedom the mechanism has.
Note:
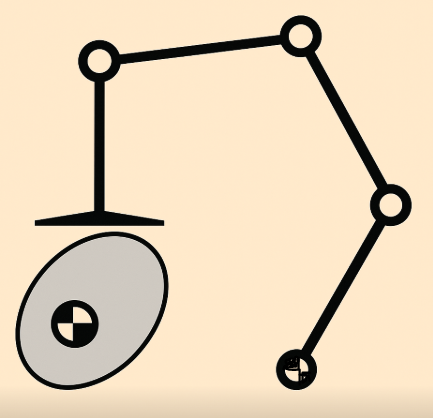
The symbol below identifies a pin or hinge fixed to the base. Essentially, it is a revolute joint with a solid axis attached to a frame. To be even clearer, it identifies a fixed rotation point.
image created with artificial intelligence, the software used is Microsoft Copilot
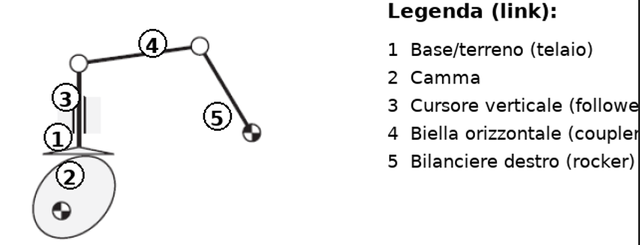
Returning to the exercise, the first thing to do is identify the bodies.
Image created with artificial intelligence, ChatGPT software used
In our system we have
01-Frame base
02-Cam
03-Vertical slider
04-Horizontal connecting rod
05-Right rocker arm
So we collect the data:
bodies n=5
lower torques j1=5
upper torques j2=1 (cam with slider)
We apply the Kutzbach/Grübler formula valid for planar systems and we will obtain the degrees of Freedom
Result
The system is monoconstrained and has only 1 degree of freedom.
Conclusions
The degrees of freedom of a mechanical system are the minimum number of independent variables necessary to describe the configuration of a mechanical system; in simple terms, they identify the mobility of the mechanical system.
Question
Did you know that Franz Kutzbach and Max Grübler were two German engineers who both worked on the theory of mechanisms and machine tools? Did you know that their theories were so similar that today the formula for calculating the degrees of freedom is called the Kutzbach–Grübler formula?

[ITALIAN]
11-08-2025 - Education - Gradi di libertà di un sistema meccanico [EN]-[IT]
[IMMAGINE]
Immagine generata con IA, Microsoft Copilot
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento citato in oggetto.
Il contesto in cui operiamo è quello della Meccanica applicata
(code notes: MOD-92)
Sistema meccanico
Il sistema meccanico è un insieme di oggetti che sono collegati tra loro ed in base a dei vincoli eseguono un movimento. L'esempio più classico può essere il sistema biella e manovella
Qui di seguito un immagine del sistema biella manovella
immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
I vincoli
Un sistema meccanico quindi è solitamente soggetto a vincoli, cioè qualcosa che costringe il movimento o che obbliga una leva a muoversi in direzioni prestabilite.
I gradi di libertà
In un sistema meccanico i gradi di libertà indicano quante variabili indipendenti sono necessarie per descrivere completamente la posizione di un sistema meccanico tenendo conto che i tipi di movimento possono essere di traslazione o di rotazione.
Comprendere bene i gradi di libertà di un sistema meccanico permette di modellare correttamente il comportamento del sistema. Questa è una fase essenziale nella progettazione meccanica.
Esercizio
Prendiamo ad esempio il sistema meccanico rappresentato nella figura qui sotto.
Cerchiamo di capire quanti gradi di libertà possiede il meccanismo rappresentato.
Nota:
Il simbolo qui sotto identifica un perno o una cerniera fissata al basamento. Sostanzialmente è un giunto rotoidale con asse solido ad un telaio e per essere ancora più chiari, identifica un punto di rotazione fisso.
immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Tornando all'esercizio, la prima cosa da fare è identificare i corpi.
immagine creata con l’intelligenza artificiale, il software usato è ChatGPT
Nel nostro sistema abbiamo
01-Base del telaio
02-La camma
03-Cursore verticale
04-Biella orizzontale
05-Bilancere destro
Quindi raccogliamo i dati:
corpi n=5
coppie inferiori j1=5
coppie superiori j2=1 (camma con pattino)
Applichiamo la formula di Kutzbach/Grübler valida per i sistemi planari e otteremo i gradi di libertà
Risultato
Il sistema è monovincolare ed a 1 solo grado di libertà.
Conclusioni
I gradi di libertà di un sistema meccanico sono il numero minimo di variabili indipendenti necessarie per descrivere la configurazione di un sistema meccanico, in parole semplici identificano la mobilità del sistema meccanico.
Domanda
Lo sapevate che Franz Kutzbach e Max Grübler erano due ingegneri tedeschi che si occuparono entrambi di teoria dei meccanismi e delle macchine utensili? Sapevate che le loro teorie erano similari tanto che oggi la formula del calcolo dei gradi di libertà porta il doppio nome nella formula di Kutzbach–Grübler?
THE END

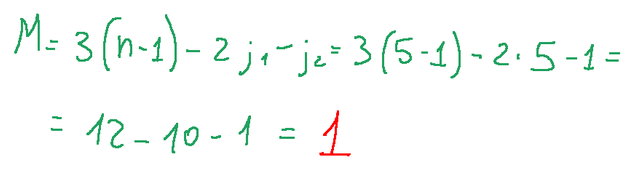
This post has been upvoted by @italygame witness curation trail
If you like our work and want to support us, please consider to approve our witness
Come and visit Italy Community
Upvoted! Thank you for supporting witness @jswit.
Your post has been supported by SC-05. We support quality posts, quality comments anywhere, and any tags