18-11-2023 - Technical contents - Internal Energy [EN]-[IT]
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
[ENGLISH]
18-11-2023 - Technical contents - Internal Energy [EN]-[IT]
Internal Energy
Each system has its own internal energy based on the state in which it is found. In thermodynamics we do not study the value of this energy so much, but rather we are interested in knowing the difference in internal energy as a consequence of a variation in the state of the system.
We can say that the internal energy of a thermodynamic system expresses the quantity of free energy of a thermodynamic system in a transformation.
Let's remember the first law of thermodynamics
The internal energy of a closed thermodynamic system is constant.
Internal energy is identified in the formulas with the letter U.
How internal energy is composed
The internal energy (U) of a thermodynamic system is given by the sum of the kinetic and potential energy of the particles that compose it.
Internal E(U) = Kinetic E + Potential E.
Example
Example dedicated to kinetic energy
Let's take a gas for example. Its particles will move with a certain speed so the internal energy depends on the speed of the particles.
Conclusions
The kinetic energy in a gas depends on the velocity of the particles so its internal energy can change depending on the velocity of the particles.
Example dedicated to potential energy.
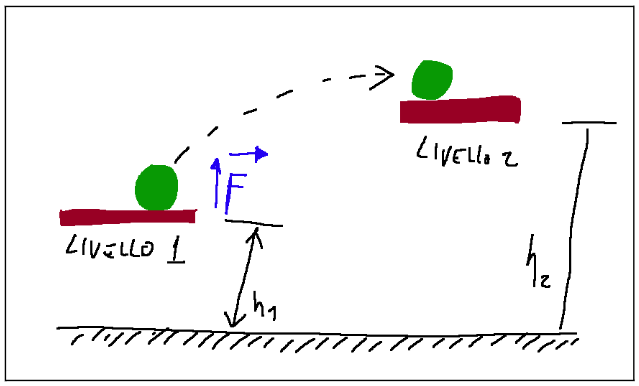
Let's take a non-deformable sphere to which the force F is applied to go from level 1 to level 2
Given the situation, let's think about the work formula which is the following
In our case we can write it in the following way where the displacement is the difference between h2 and h1
Let us now think about internal energy, or rather potential energy.
The sphere is initially found on a lower level, while in the end it is found on level 2 which has a greater height. Let's now create the formula that identifies its initial potential energy (Ui) and final potential energy (Uf)
From these two formulas we can deduce that Uf is greater than Ui because the height h changes, which is greater on level 2.
So Uf is different from Ui, which means that one of the physical quantities of the sphere has changed. In this case its potential energy.
Conclusions
The potential energy of a sphere increases if it is at a greater height, so its internal energy changes as the height varies.

[ITALIAN]
18-11-2023 - Contenuti tecnici - Energia Interna [EN]-[IT]
Energia Interna
Ogni sistema ha una sua energia interna in base allo stato in cui si trova. Nella termodinamica non si studia tanto il valore di questa energia, ma piuttosto interessa conoscere la differenza di energia interna in conseguenza di una variazione dello stato del sistema.
Possiamo dire che l’energia interna di un sistema termodinamico esprime la quantità di energia libera di un sistema termodinamico in una trasformazione.
Ricordiamo il primo principio della termodinamica
L’energia interna di un sistema termodinamico chiuso è costante.
L’energia interna viene identificata nelle formule con le lettera U.
Come è composta l’energia interna
L’energia interna (U) di un sistema termodinamico è data dalla somma dell’energia cinetica e potenziale delle particelle che lo compongono.
E interna(U) = E cinetica + E potenziale.
Esempio
Esempio dedicato all’energia cinetica
Prendiamo ad esempio un gas. Le sue particelle si muoveranno con una certa velocità quindi l’energia interna dipende dalla velocità delle particelle.
Conclusioni
L’energia cinetica in un gas dipende dalla velocità delle particelle quindi la sua energia interna può cambiare a seconda della velocità delle particelle.
Esempio dedicato all’energia potenziale.
Prendiamo una sfera indeformabile a cui viene applicata la forza F per passare dal livello 1 al livello 2
Vista la situazione pensiamo alla formula del lavoro che è la seguente
Nel nostro caso la possiamo scrivere nella seguente maniera dove lo spostamento è la differenza tra h2 e h1
Ragioniamo ora sull’energia interna, o meglio sull’energia potenziale.
La sfera inizialmente si trova su un livello più basso, mentre alla fine si trova appunto sul livello 2 che ha un altezza maggiore. Vediamo ora di creare la formula che identifica la sua energia potenziale iniziale (Ui) e quella finale (Uf)
Da queste due formule possiamo dedurre che Uf è maggiore di Ui perché cambia proprio l’altezza h, che sul livello 2 è maggiore.
Quindi Uf è diverso da Ui, il che significa che una delle grandezze fisiche della sfera è cambiata. In questo caso la sua energia potenziale.
Conclusioni
L’energia potenziale di una sfera aumenta se si trova su un altezza maggiore, quindi la sua energia interna cambia con il variare dell’altezza.
THE END

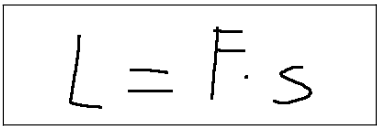
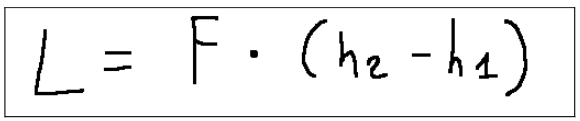

Interessante post
Ieri ho provato a spiegare a mio figlio di 7 anni questo concetto dell’energia potenziale, cioè in quale nei due casi la sfera abbia maggior energia potenziale. Anche se non ha compreso bene il significato di energia potenziale ha compreso che, siccome il calcolo dell’energia potenziale dipende dall’altezza, egli ha pensato che la pallina ad altezza maggiore avesse appunto un valore di energia maggiore. Mi ha stupito. Non ha compreso nulla di questo meccanismo, ma ha effetuato un ragionamento logico che lo ha portato a dare la soluzione corretta.