30-06-2025-Exercise-Succession of Cauchy [EN]-[IT]
Cover background image generated with AI, software used: copilot microsoft
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
[ENGLISH]
30-06-2025-Exercise-Succession of Cauchy [EN]-[IT]
Image generated with IA, Microsoft Copilot
With this post I would like to provide some short notions regarding the topic mentioned in question by carrying out exercises.
The context in which we operate is that of the mathematical analysis
(Code Notes: Mod-80)
Couchy's succession
Basic concepts to perform the exercise
Subdexation
A subsucencement is a succession achieved by another succession by choosing some of its terms, while maintaining the original order.
In other words we can say that, given a succession
A subtosuccession is a succession of the type
Where NK is a strictly growing succession of natural numbers, that is N1 <n3 <....
Which of these considerations is correct?
1-pay for the point (0.1) and is unlimited
2-pay for (1.0) and is growing and unlimited
3-pay for the point (0.1) and is positive and growing
2-pay for (1.0) and is positive
Cauchy's successions
When we talk about a Cauchy succession we talk about a succession in which the terms become arbitrarily close to each other as the index grows.
In other words in a succession of Cauchy, the terms tighten more and more.
Below is a classic example of a Cauchy succession.
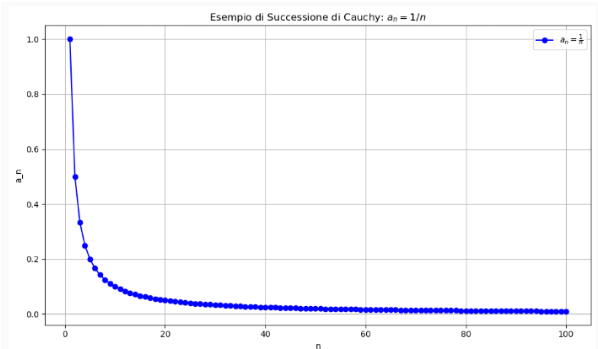
Let's consider the graph of the following succession.
From this succession we get the following graphic designer.
Image generated with IA, Microsoft Copilot
From this graph we see that in this particular succession the points are increasingly approaching zero as N grows. The points never reach zero, but the distance between the terms becomes smaller and smaller and this is the typical behavior of Cauchy's successions.
** Exercise 01 **
Check that the following succession is a Cauchy succession.
development
-1-
Below is the first step to take the exercise. We build the expression of the difference.
-2-
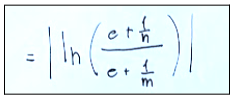
In the second step we use the use of the properties of logarithms.
-3-
Now we observe that when n, m → ∞, both 1/n → 0 and 1/m → 0, then:
-4-
Now we can make the esteem for the difference
-5-
Given that …
When n, m → ∞, then also ...
So it's a Cauchy succession
Result
Since the terms arbitrarily become close to each other for N, sufficiently large, we can say that the succession proposed by the exercise is a succession of Cauchy.
Conclusions
When we go into pure mathematics, Cauchy's successions become fundamental. They are very important for numerical analysis, scientific calculation, machine learning, signal theory and in engineering.
Request
Did you know that Cauchy (1789-1857) was one of the first to formalize the concept of limit? Did you know it was an extremely prolific mathematician and that he wrote more than 800 articles and 5 books?

[ITALIAN]
30-06-2025 - Esercizio - Successione di Cauchy [EN]-[IT]
Immagine generata con IA, Microsoft Copilot
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento citato in oggetto svolgendo degli esercizi.
Il contesto in cui operiamo è quello della Analisi Matematica
(code notes: MOD-80)
Successione di Cauchy
Concetti base per svolgere l’esercizio
sottosuccessione
Una sottosuccessione è una successione ottenuta da un’altra successione scegliendo alcuni dei suoi termini, mantenendo però l’ordine originale.
In altre parole possiamo dire che, data una successione
una sottosuccessione è una successione del tipo
Dove nk è una successione strettamente crescente di numeri naturali, cioè n1<n2<n3<....
Quale di queste considerazioni è corretta?
1-passa per il punto (0,1) ed è illimitata
2-passa per (1,0) ed è crescente e illimitata
3-passa per il punto (0,1) ed è positiva e crescente
2-passa per (1,0) ed è positiva
Successioni di Cauchy
Quando parliamo di una successione di Cauchy parliamo di una successione in cui i termini diventano arbitrariamente vicini tra loro man mano che l’indice cresce.
In altre parole in una successione di Cauchy, i termini si stringono sempre di più.
Qui di seguito è mostrato un esempio classico di una successione di Cauchy.
Prendiamo in considerazione il grafico della seguente successione.
Da questa successione otteniamo il seguente grafico.
Immagine generata con IA, Microsoft Copilot
Da questo grafico vediamo che in questa particolare successione i punti si avvicinano sempre di più allo zero man mano che n cresce. I punti non raggiungono mai lo zero, ma la distanza tra i termini diventa sempre più piccola e questo è il tipico comportamento delle successioni di Cauchy.
Esercizio 01
Verificare che la seguente successione sia una successione di Cauchy.
sviluppo
-1-
Qui di seguito il primo passo da compiere per svolgere l’esercizio. Costruiamo l’espressione della differenza.
-2-
Al secondo passaggio sfruttiamo l’uso delle proprietà dei logaritmi.
-3-
Ora osserviamo che quando n,m → ∞, sia 1/n→0 che 1/m→0, quindi:
-4-
Ora possiamo fare la stima della differenza
-5-
Dato che …
quando n,m → ∞, allora anche…
Quindi è una successione di Cauchy
Risultato
Siccome i termini diventano arbitrariamente vicini tra loro per n,m sufficientemente grandi, possiamo dire che la successione proposta dall’esercizio è una successione di Cauchy.
Conclusioni
Quando ci addentriamo nella matematica pura le successioni di Cauchy diventano fondamentali. Sono importantissime per l'analisi numerica, il calcolo scientifico, machine Learning, teoria dei segnali ed in ingegneria.
Domanda
Lo sapevate che Cauchy (1789-1857) fu uno dei primi a formalizzare il concetto di limite? Sapevate che era un matematico estremamente prolifico e che scrisse più di 800 articoli e 5 libri?
THE END

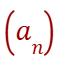
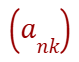
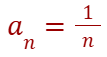
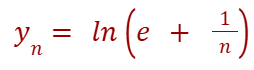
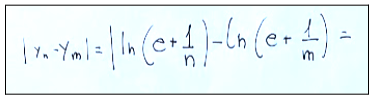
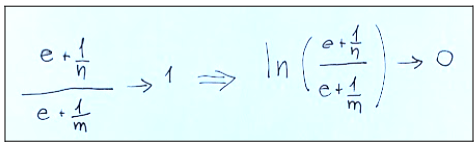
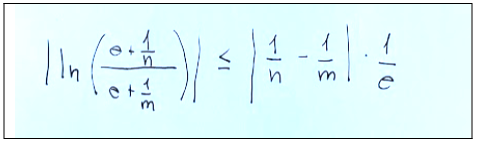

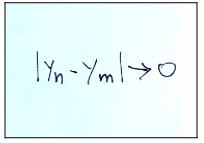

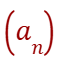
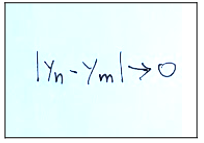
This post has been upvoted by @italygame witness curation trail
If you like our work and want to support us, please consider to approve our witness
Come and visit Italy Community
Upvoted! Thank you for supporting witness @jswit.