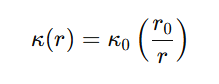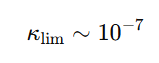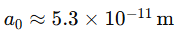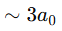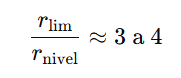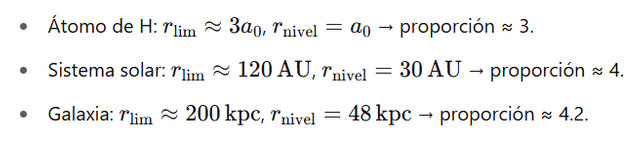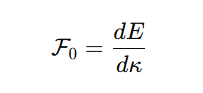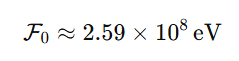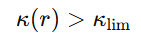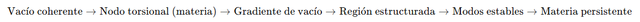El átomo de hidrógeno, el sistema solar y la estructura galáctica: Una interpretación diferente de la materia oscura
Introducción y motivación del paralelismo
¿Y si el mismo principio que estructura un átomo también define los límites del sistema solar y de una galaxia?
Esta idea, en apariencia poética o especulativa, puede ser examinada rigurosamente dentro de la el contexto que venimos desarrollando. Según esta teoría, el vacío cuántico no es pasivo, sino que posee una estructura dinámica que determina qué configuraciones de materia y energía pueden sostenerse de forma estable. Esa estructura se cuantifica mediante una función espacial: el acoplamiento torsional efectivo, denotado por:
k ( r )
La hipótesis que exploraremos aquí es la siguiente:
“Existen límites torsionales naturales definidos por la estructura del vacío, que marcan el fin de los niveles ligados posibles en cualquier sistema con un nodo central de energía.”
Esto incluye, por ejemplo:
- El protón en el átomo de hidrógeno.
- El Sol en el sistema solar.
- El centro galáctico en una galaxia espiral.
Y en cada uno de estos sistemas, podríamos identificar:
- Una región de niveles ligados.
- Un límite estructural más allá del cual no se mantienen orbitas o modos.
- Una relación proporcional entre el último nivel ligado y ese límite.
El modelo básico – cómo se calcula la torsión estructural
La TEV asume que el vacío reacciona a la energía presente formando estructuras de torsión. El acoplamiento torsional decrece radialmente desde una fuente central según:
donde:
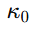es el valor de referencia a una distancia 
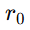cercana al nodo.- r es la distancia al centro.
- Este perfil se deriva de una simetría radial conservando el “flujo torsional”.
En todos los sistemas, se postula la existencia de un umbral universal de torsión por debajo del cual no se pueden formar modos ligados:
Este valor representa el “borde natural” de la coherencia estructural. Si un sistema tiene una caída de k ( r ) que cruza ese umbral, no podrá sostener estructuras estables más allá.
Comparación estructural – tres escalas, una misma lógica
El esquema general
Vamos a comparar tres sistemas distintos:
| Sistema | Nodo central | Región de niveles ligados | Límite torsional observado |
|---|---|---|---|
| Átomo de H | Protón | Radio de Bohr: | Nube atómica difusa  |
| Sistema solar | Sol | Neptuno (30 AU) | Heliopausa (~120 AU) |
| Galaxia espiral | Bulbo galáctico | Fin del disco H I (~48 kpc) | Halo de materia oscura (~200 kpc) |
En todos los casos:
- Existe un centro energético que actúa como nodo de torsión.
- Se forma una región estructurada, donde existen niveles ligados (órbitas, modos).
- Existe un límite observable más allá del cual no hay estructuras estables, coherente con el punto donde:
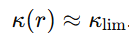
Veamos ahora las proporciones numéricas con más detalle.
3.2 Proporción entre nivel ligado y límite torsional
En los tres sistemas, si tomamos el radio del último nivel ligado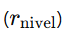 
y lo comparamos con el límite 
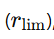, se obtiene:
Estas proporciones emergen al aplicar la misma ley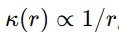 
, y usar una única constante universal.
¿Y cómo se relaciona todo esto con energía? La constante estructural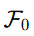 
— energía por unidad de torsión
La constante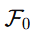 
surge de una necesidad crítica dentro de la TEV: cuantificar cuánta energía estructural se requiere para sostener un cambio diferencial en la rigidez del vacío (es decir, en k).
Imaginá que el vacío tiene una especie de elasticidad interna: cuanto más lo deformás (mayor k), más energía se requiere para mantener esa deformación. Así como en un resorte la energía almacenada depende de la compresión, aquí depende del grado de torsión estructural.
La relación aproximada que se propuso es:
Donde:
- dE es el cambio de energía estructural.
- dk es el cambio de rigidez estructural del vacío.
Esta constante puede pensarse como una especie de "pendiente" que une energía y estructura torsional.
¿Cómo se obtiene?
La estimación de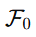 
no provino de la observación astronómica directa, sino de un problema que aparece en física nuclear y la cosmología: la sobreproducción esperada de litio-7 en la nucleosíntesis primordial. La TEV propone que las condiciones del vacío en el universo temprano modificaron el umbral de estabilidad estructural para ciertos núcleos, como el litio-7, a través de un acoplamiento k que variaba con la densidad del plasma y la escala local del vacío.
Mediante el análisis de la energía asociada a esa transición estructural en el vacío primitivo —necesaria para que el litio-7 no se estabilizara con la frecuencia esperada— se calculó que:
Este valor fue ajustado una única vez con base en las observaciones cosmológicas (el llamado “problema del litio”) y no se modificó al aplicarlo en otras escalas.
¿Por qué es tan importante?
Porque cuando se usa esta misma constante para predecir el límite torsional del sistema solar y de galaxias espirales, los resultados obtenidos coinciden con los bordes observados en la heliopausa y en el radio virial.
Es decir:
Una constante estructural definida en el universo temprano explica por qué Neptuno es el último planeta con órbita estable y también por qué el disco galáctico se corta donde lo hace.
Excelente idea. Vamos a cerrar esta sección 3.3 con una expansión adicional que vincule directamente esta estructura torsional del vacío con el fenómeno conocido como materia oscura, tal como se manifiesta en los halos galácticos.
¿Cómo se relaciona esto con la materia oscura?
En la cosmología actual, los astrónomos observan que las galaxias espirales giran más rápido en sus bordes de lo que predeciría la gravedad newtoniana basada solo en la materia visible. Para explicar esto, se postula la existencia de una materia oscura invisible, que forma un halo extendido alrededor de la galaxia y proporciona la gravedad necesaria para sostener esas velocidades de rotación.
La TEV propone una alternativa estructural: lo que observamos como "materia oscura" podría ser, en realidad, un efecto emergente de la rigidez torsional del vacío.
La clave está en que, según la TEV:
- El vacío posee una estructura activa, con una rigidez espacial que decae con la distancia:
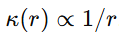
- Mientras
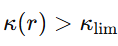, el vacío puede sostener modos ligados estructurales: órbitas planetarias, discos galácticos, halos estables. - Más allá de ese límite, ya no pueden sostenerse estructuras coherentes; la materia no se organiza, y no hay más crecimiento.
Así, la presencia de un “halo” no sería evidencia de una nueva clase de materia, sino simplemente la manifestación final del campo de coherencia torsional generado por el nodo central (la galaxia) sobre el vacío.
Es decir:
Lo que hoy llamamos “materia oscura galáctica” podría ser una fase del vacío estructurado, sin necesidad de partículas nuevas.
Más aún: usando la constante estructural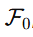 
, se puede predecir el punto en que el gradiente torsional cae por debajo del umbral 
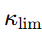, y ese punto coincide con el radio del halo galáctico observado (del orden de 200 kpc para galaxias como NGC 3198).
¿El vacío define a la materia o la materia configura el vacío? Vacío y materia en la TEV
Una de las preguntas más profundas que surgen al estudiar la Torsión Estructural del Vacío (TEV) es:
¿Es la materia la que le da forma al vacío, o es el vacío el que da forma a la materia?
En la física clásica y cuántica, el vacío es a menudo el telón de fondo: algo pasivo. En la TEV, en cambio, el vacío es activo, estructurado y dinámico, y su relación con la materia es mutuamente estructurante.
Fase 1: El vacío estructura a la materia
La TEV parte de una premisa clave:
Para que una partícula o una estructura estable (como un planeta, un átomo o una estrella) pueda existir, el vacío debe tener una torsión estructural mínima. Esta condición se expresa como:
donde k (r) es el acoplamiento estructural local del vacío, y K lim es el umbral mínimo necesario para que exista una estructura estable.
Así, la materia es una manifestación coherente del vacío estructurado. No es un "algo" flotando en el vacío, sino una forma estable de la energía organizada dentro de una región del vacío que cumple ciertas condiciones de torsión.
En este sentido, el vacío le da forma a la materia.
Solo donde el vacío tiene suficiente rigidez pueden existir estructuras coherentes.
Fase 2: La materia configura el vacío
Una vez que surge una estructura (como un núcleo atómico, una estrella o una galaxia), esta deforma y organiza el vacío a su alrededor:
- Actúa como un nodo de torsión.
- Genera un gradiente estructural
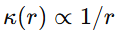. - Establece una jerarquía de niveles: órbitas atómicas, sistemas solares, discos galácticos, etc.
Este gradiente de torsión no solo estructura el entorno sino que también establece límites: más allá de cierto radio, el vacío se vuelve demasiado débil para sostener más modos ligados. Ahí termina la materia visible y aparece lo que hoy llamamos materia oscura.
En este sentido, la materia también estructura al vacío.
La retroalimentación entre vacío y materia
Esta relación no es lineal ni jerárquica, sino recursiva y dinámica. Podríamos representarla así:
Cada etapa sostiene y retroalimenta a la anterior. La materia necesita de un vacío estructurado para existir, y a su vez, mantiene y ordena la estructura de ese vacío.